Content
Scroll down and you will see all!
Shortcuts:
- Obtuse Package
- Customizing Manipulate's Autorun
- Tetration
- DivideTriangle
- TaggedCells Package
- SetFaceAndFont
- Gallery
Obtuse Package
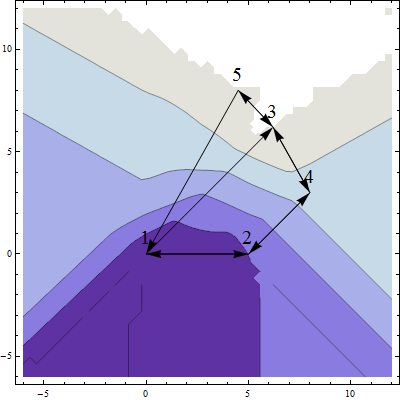
This package contains routines and tools for obtuse angle shadowing networks and distance-based interpolation between scattered, multidimensional points. Four variants of distance-based interpolation can be compared with (coordinate-based) 2D Delaunay interpolation.
If you deal with experimental data in any form, it is a very common case that you can represent the data as a set of numbered scattered points in an abstract point space. You might have a lot of numerical information about the cloud of points, but to be able to gain knowledge, you should look for structures, patterns and relations in this cloud. You should look for outliers, for typical points and point neighborhoods, for shapes like threads, sheets and holes, etc. Suppose, that you have such a set of scattered points in any or an unknown number of dimensions, and that maybe you do not know their coordinates, but you know how to calculate the distance between them. To be able to learn anything about your diffuse cloud of points, it is very useful to have tools to categorize the relations between the points and the shape of the cloud. You can use the distance information to define an obtuse-angle shadowing network connecting nearby points in the set. If you have a function defined on this point set, you might use this network to define a distance-based interpolation function to estimate the function value for a new point of the same kind. Such networks and this kind of interpolation should have applications in various fields, for example image processing and machine learning. The Obtuse package provides Mathematica functions to find and investigate such networks, and to use them for interpolation.
The Obtuse package adds five interpolation methods to the Mathematica Interpolation command:
- The Delaunay interpolation method to the Interpolation command is a coordinate-based interpolation method, here allowing only 2D-points. The method is based on Delaunay triangulation of the control points and triangular interpolation inside the Delaunay triangles.
The other four interpolation methods are distance-based. The distance-based interpolation methods could be applied to a large set of geometries, including multi-dimensional, periodic and regions with cuts, as long as the relevant distance function is specified.
 |
| Interpolation in the color space of a picture is possible |
- The Voronoi interpolation method to the Interpolation command returns the function value of the nearest control point from the interpolation point. The function is thus constant in regions. The function values could thus be almost any kind of valid Mathematica statements. This function is useful if you want to construct answers to questions like "What is the name and address of the closest restaurant", but could also be useful in machine learning.
- The Shepard interpolation method is included just for historical reasons and as comparison, and should not be used for serious work without careful consideration. The Shepard interpolation is using the distance to a control point, raised to the inverse ShepardPower parameter, as a weight for the function value in the control point. The weights are then normalized to have 1 as their sum.
- The RBF interpolation method can be seen as an improvement of the Shepard interpolation. We let each control point be the center for one radial base function (a function where the value is determined by the distance to the center), and form a linear combination of all these functions. We choose the weights in this linear combination in such a way that it takes the function values in the control points. Since we have the same number of weight as we have function values, we should in general have a well-specified equation system to solve. The radial base functions could be chosen in various ways, but a fundamental property should be that they are finite but non-zero at origin and smoothly decreasing or increasing outwards.
- The ObtuseAngle interpolation method is based on the ObtuseAngle connection list.
Download the Obtuse package file obtuse004.zip and unpack according to the readme file inside.
In Mathematica 8 there is a "compat" warning when the Obtuse package is loaded. This warning can be ignored.
Obtuse003.zip contains minor cosmetic improvements compared to the earlier version obtuse002.zip
In Obtuse004.zip all uses of HierarchicalClustering`DistanceMatrix are replaced by internal package code. In this way the treatment of symbolic variables improves. A bug related to symbolic variables is removed. The interpolation function for the RBF method can be differentiated symbolically.
You might register the package by sending me an email containing the words "REGISTER OBTUSE" and your email address. Feedback and user reports are appreciated.
Even if you do not have Mathematica available, you might check the online documentation, or check the related demonstration Obtuse Angle Shadowing Networks and Distance-Based Interpolation from the Wolfram Demonstrations Project by Ingolf Dahl
Customizing Manipulate's Autorun
If you are not satisfied with how the Autorun feature of Manipulate runs the controls sequencially, and want to shake all the controls simultaneously, you might appreciate a Mathematica notebook about this. Download CustomizingManipulatesAutorun.nb! You will also learn how to annotate the Autorun feature. And when you have tasted blood, you might want customize the Animate Bookmarks feature too. Download CustomizingManipulatesAnimateBookmarks.nb!
These files were updated up to my current understanding 2010-09-14.
Tetration
Addition, multiplication, exponentiation, ... What comes next? Tetration, or PowerTower in the language of Mathematica. Here is a notebook with the routines for extending the exponent to real positive values: http://www.familydahl.se/mathematica/PowerTower.nb. The current version is created 2006-12-21, with added theory and graphs and changed routines. If you do not have Mathematica available, you might download a notebook reader from http://www.wolfram.com/products/mathreader/ .
More to come...
DivideTriangle
A routine to split a triangle, or a list of triangles, into small triangles with all sides less than d: http://www.familydahl.se/mathematica/DivideTriangle.nb.
TaggedCells Package (still beta...)
By default Mathematica notebooks are organized linearly, with output
cells following corresponding input cells. Sometimes it is useful to have larger
freedom in how to write and read. We maybe want to rewrite the same cell several
times, for example if we want a status window to monitor an on-going process. Or
we might want to write to the same cell from several positions in a notebook. Or
we might want to collect the results from a complicated calculation in a nice
formatted report. Mathematica provides a mechanism to "tag" cells with
names. Or maybe create a game? This package provides routines to utilize this in a convenient way.
Some routines is also provided in this package to enter input to Mathematica
programs in some different ways plus a few utilities. The functions in the
package have full option and help support.
Some highlights:
- The possibility to make 3D animations where the viewpoint can be changed dynamically during executions.
- The possibility to get Graphics coordinates from inside a program loop
- A rudimentary Mathematica-Aided drawing program. Yes, fully inside a Mathematica notebook, no Java stuff here. Although primitive, you might use it to paste your Mathematica formulas into your own Mathematica graphics.
- FormOptionSequence is an modification of Utilities`FilterOptions` with enhanced functionality.
Available commands and options: AnimateToClosedGroup, AppendToTaggedCell, DeleteTaggedCell, EvaluateTaggedCell, EvaluateWithTaggedCellButton, ExpressionCell, ExpressionToTaggedCell, FilterOptionList, FormOptionSequence, GraphicBoxDataCell, GraphicsCell, GraphicsCellGroup, InterruptButton, InterruptButtonCell, InterruptWithTaggedCellButton, InvisibleNotebook, NotebookReadTaggedCell, OptionalNotebookOpen, PauseFunction, PrintToTaggedCell, ReadCellInformation, ReadCellInformationTaggedCell, ReadCellSerialNumbers, ReadCellSerialNumberTaggedCell, ReadCursorPosition, ReadMousePad, ReadOptionTaggedCell, ReadViewPoint, RemoveDoublets, ReplaceOptionTaggedCell, SelectTaggedCell, ShowTo3DBoxedCell, ShowToTaggedCell, TaggedCellNotebook, TargetNotebook, TextDataCell, TextDataToTaggedCell
Please help me to test this package, and send feedback to ingolf.dahl@telia.com ! The package is intended for Mathematica 5.1 and 5.2, and has been developed on a Windows XP computer.
(The PrintToTagggedCell notebook, earlier available here, is now made obsolete.)
Download from http://www.familydahl.s/mathematica/TaggedCells0p93.zip and unpack according to the readme file inside.
Version 0.93 (beta) published June 14, 2006.
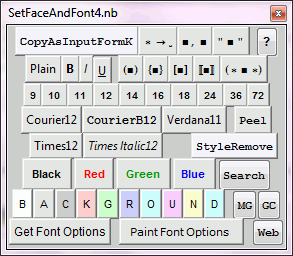 SetFaceAndFont, version 2.1
SetFaceAndFont, version 2.1
A palette to change face and font, but also to convert to input form, to add and remove brackets and parentheses, and to search the Mathematica online help, the Mathematica forums (e.g. MathGroup) and the entire web (possibly also including your own desktop). Comes with help files integrated with the Mathematica help. The palette is intended for Mathematica 6 and higher, and has been developed on a Windows 7 computer.
Download SetFaceAndFont211.zip and unpack according to the readme file inside.
Version 2.1.1 published September 1, 2010
Some font buttons replaced to reflect the new Help style in Mathematica.
The GC button added for Mathematica code search.
Font size 11 added.
The Search button now searches the whole wolfram.com site.
The source code is now included in the zip file (Jan 11, 2011).
Version 2.0.4 published September 14, 2005, for Mathematica 5.1 and 5.2
Changes from version 2.0.3 to 2.0.4:
1. Peel changed to return executable cell from a SurfaceGraphics cell
rendered as a RealTime3D cell. CopyAsInputFormK, "▪"
and StyleRemove buttons corrected in behavior in relation to a
SurfaceGraphics cell rendered as a RealTime3D cell. Most users do not use these
features. If you are curious about such cells, see
http://forums.wolfram.com/mathgroup/archive/2001/Apr/msg00346.html.
2. Some entries have been added to Help Master Index and some entries have been
changed..
3. The language in the search result pages for Search, MG, Web
buttons has been changed to English.
Gallery
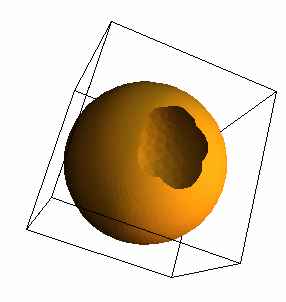 Golden bowl in dynamic 3D (requires
Java, 610 kB large file which might take some time to load.)
Golden bowl in dynamic 3D (requires
Java, 610 kB large file which might take some time to load.)
To the homepage of Ingolf Dahl.
Last time this page was changed was 2011-01-26